Trees

Definition and Terminology

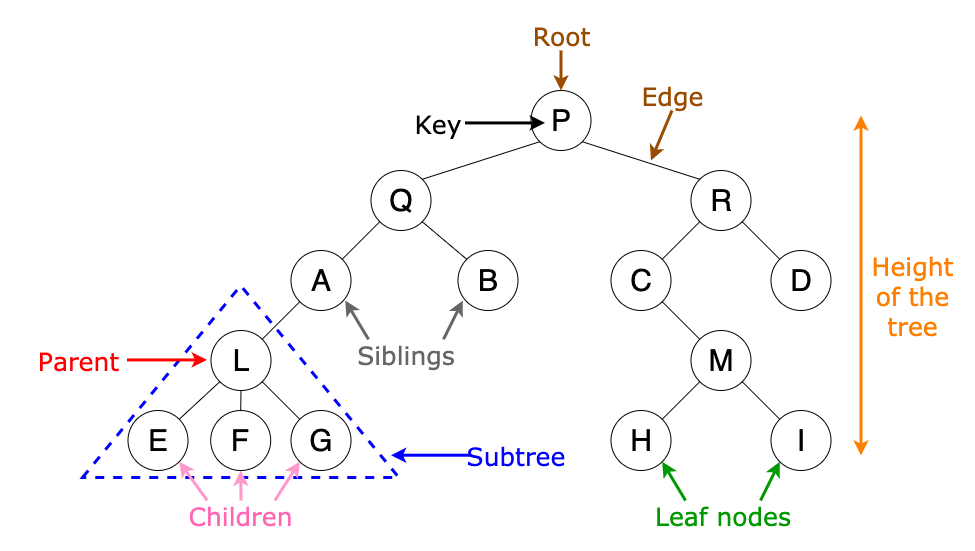
Tree data structure to represent hierarchical data its a recursive data structure. A tree is either:
1. Empty
2. Have a root value connected to any number pf the trees, called the subtrees of the tree
Size of a tree is the number of values in the tree.
Leaf — a value with no subtrees
Internal value (opposite to leaf), its a value that has at least one subtree
Height of tree is the length of the longest path form tis room to one of its leaves
Children of a value are all values directly connected underneath that value
- Descendants of value are its children, the children of its children etc
Parent of a value is the value immediately above and connected to it. Each value in a tree has exactly one parent, except the root
- Ancestors of a value are its parents, the parent of its parent etc
A value is never a child or parent of itself

Tree implementation

class Tree:
    """A recursive tree data structure.
    
    Representation Invariants:
        - self._root is not None or self._subtrees == []
    """
    # Private Instance Attributes:
    #   - _root:
    #       The item stored at this tree's root, or None if the tree is empty.
    #   - _subtrees:
    #       The list of subtrees of this tree. This attribute is empty when
    #       self._root is None (representing an empty tree). 
    #		However, this attribute may be empty when self._root is not None,
    #       which represents a tree consisting of just one item.
    _root: Optional[Any]
    _subtrees: list[Tree]
        
    def __init__(self, root: Optional[Any], subtrees: list[Tree]) -> None:
        """Initialize a new Tree with the given root value and subtress.
        
        If root is None, the tree is empty
        
        Preconditions:
        	- root is not none or subtrees ==[]
        """
        self._root = root
        self._subtrees == subtrees
        
    def is_empty(self) -> bool:
        """Return whether this tree is empty"""
        return self._root is None

Creates an empty tree when root is None
A tree with a value and the given subtrees
Root is not None, while subtrees are empty — a tree with a single root value

Tree recursion

Code template:

class Tree:
    def method(self) -> ...:
        if self.is_empty():
            (...)
        elif self._root (...):  # explicit self._root case
            (...)
        else:
            for subtree in self.subtrees:
                (...) subtree.method() (...)
            (...)

Ex. Tree size

Let $T$ be a tree, and let $s i ze$ be a function mapping any tree to its size
- If $T$ is empty, then its size is 0: $s i ze (T) = 0$
- If $T$ is non-empty, then it consists of a root value and collection of subtrees $T_{0}, T_{1}, \dots T_{k - 1}$ (for some $k \in N$ ). Then, the size of $T$ is the $s u m$ of the sizes of its subtrees plus 1 for the root
  $s i ze (T) = 1 + i = 0 \sum k - 1 s i ze (T_{i})$

Combine these two cases to write a recursive mathematical definition for $s i ze$ function

s i ze (T) = {0, 1 + \sum_{i = 0}^{k - 1} s i ze (T_{i}) if T is empty if T has subtrees T_{0}, T_{1}, \dots T_{k - 1}

class Tree:
    def __len__(self) -> int:
        """Return the number of items contained in this tree.
        
        >>> t1 = Tree(None, [])
        >>> len(t1)
        0
        >>> t2 = Tree(3, [Tree(4, []), Tree(1, [])])
        >>> len(t2)
        3
        """
        if self.is_empty():  # tree is empty
            return 0
        elif self._subtrees == []:  # tree is a single item
            return 1
        else:  # tree has at least one subtree
            size_so_far = 1
            for subtree in self._subtrees:
                size_so_far += subtree.__len__()
            return size_so_far

Ex. `Tree.str`

f-Strings format: f'{variable}' == str.format(variable)

>>> name = "Mel"
>>> f"Hello, {name}"
'Hello, Mel'

Start with the value of root, then recursively add on the __str__ for each of the subtrees
Base case returns an empty string
Pass in an extra parameter for the depth of the current tree, to add a corresponding number of indents before each value in the str that is returned

Make a parameter optional by giving it a default value: depth: int = 0 to define a default value for depth

Since depth is optional, if assigned a specific value (ex. t.__str__(5)) then the depth would have the parameter to 5, otherwise, if not specified (ex. t.__str__()) then the depth parameter is assigned to 0
All optional parameter must appear after all of the required parameters in the function header
DO NOT use mutable values like lists for the optional parameters

def __str__(self, depth: int = 0) -> str:
    """Return a string represention of this tree
    
    The indentation level is specified by the <depth> parameter
    """
    if self.is_empty():
        return ''
    else:
        # use newlines ('\n') to separate the different values
        s = '	' * depth +  f'{self.root}\n'
        for subtree in self._subtrees:
            # the 'depth' argument to the recursive call is modified
            s += subtree.__str__(depth + 1)  # equivalent ot str(subtree)
        return s

Traversal orders

Left-to-right preorder
1. First it visits the root value
2. Then it recursively visits each of its subtrees, in left-to-right order

Left-to-right postorder

First recursively visits each of its subtrees
Then visits the root value

def __str__(self, depth: int = 0) -> str:
    """Return a string represention of this tree
    
    The indentation level is specified by the <depth> parameter
    """
    if self.is_empty():
        return ''
    else:
        # use newlines ('\n') to separate the different values
        s = ''
        for subtree in self._subtrees:
            # the 'depth' argument to the recursive call is modified
            s += subtree.__str__(depth + 1)  # equivalent ot str(subtree)
            
        s += '	' * depth +  f'{self.root}\n'
        return s

Mutating Trees (value-based deletion)

Start with the recursion template, and impolite the base case:

class Tree:
    def remove(self, item: Any) -> bool:
        """..."""
        if self.is_empty():
            return False # item cannot be in the tree
        else:
            (...)
            for subtree in self.subtrees:
                (...) subtree.method() (...)
            (...)

First check the root, the if not, recurse on the subtrees

Deleting the root requires a little more step, use Tree._delete_root to hold on for now
Keep in mind that this function requires a return statement, include it in the recursions

class Tree:
    def remove(self, item: Any) -> bool:
        """..."""
        if self.is_empty():
            return False 
        elif: self._root == item:
                self._delete_root()  # delete the root
        else:
            for subtree in self.subtrees:
                deleted = subtree.remove(item)
                if deleted:
                    return True
            # The item does not appear in this tree
            return False

Implement the Tree._delete_root function

If this tree has subtrees, then the _root cannot be set to None (divide into cases)
Pick the rightmost subtree, and “promote” its root and subtrees by moving them up a level

class Tree:
    def _delete_root(self) -> None:
        """Remove the root item of this tree.
 
        Preconditions:
            - not self.is_empty()
        """
        if self._subtrees == []:
            self._root = None
        else:
            # Get the last subtree in this tree.
            chosen_subtree = self._subtrees.pop()
 
            self._root = chosen_subtree._root
            self._subtrees.extend(chosen_subtree._subtrees)

Curren problem: when deleted a leaf, it would result in a empty tree (parent would contain an empty tree in its subtree list)

Remove the deleted empty subtree from its parent’s subtree list

It is extremely dangerous to mutate the list during loops. This would interferes with he iterations of the loop that is underway. It is allowed here because immediately after the mutation, the loop would be stoped by the return statement

class Tree:
    def remove(self, item: Any) -> bool:
        """A recursive tree data structure.
 
    	Representation Invariants:
        - self._root is not None or self._subtrees == []
        """
        if self.is_empty():
            return False 
        elif: self._root == item:
                self._delete_root()  # delete the root
        else:
            for subtree in self.subtrees:
                deleted = subtree.remove(item)
                if deleted and subtree.is_empty():
                    self._subtrees.remove(subtree)
                    # item was deleted and subtree is empty
                    return True
                elif deleted:
                    # item was deleted and subtree is NOT empty
                    return True
            # The item does not appear in this tree
            return False

Implicit assumptions are bad, explicit representation invariants are good for communication

#ADD
class Tree:
    """A recursive tree data structure.
 
    Representation Invariants:
        - self._root is not None or self._subtrees == []
        - all(not subtree.is_empty() for subtree in self._subtrees)  # NEW
    """

Running-Time Analysis for Tree Operations

Analyzing `Tree.len`

class Tree:
    def __len__(self) -> int:
        """Return the number of items contained in this tree.
        """
        if self.is_empty():
            return 0
        else:
            size_so_far = 1
            for subtree in self._subtrees:
                size_so_far += subtree.__len__()
            return size_so_far

Let $n$ be the size of self (the num of items in tree), assume $n > 0$ so the else branch execute

Analyzing the structure of recursive calls

Suppose a tree defined like this:

Make the initial call for the root, call (A) would then later generate 3 recursive calls on each of this subtrees (B), (C), (D)

The recursive call on (B) would then generate 2 more recursive calls on (E), (F)

Both (E) and (F) is a leaf, no more recursive calls would be generated

The call on (C) would then trigger 2 more recursive calls on (G), (H)

(G) is a leaf, recursion ends for this branch

The call on (H) would then lead to one more recursive call on (J)

(J) is a leaf, the recursion ends for this branch

The call on (D) would lead to the recursive call on (I)

(I) is a leaf, no more recursive call would happen

Takeaway: the structure of the recursive calls exactly follows the structure of the tree
- With is example of 10 items, 10 calls were called on the whole tree.

Analyzing the non-recursive part of each call

Count the number of steps performed by a single recursive call, then add those up across al the different recursive calls that are made
- Assuming each recursive call takes constant time, count the non-recursive steps in the code
- 1 step for the initial assignment statement
- $k$ Steps for the lop, where $k$ is the number of subtree in the tree (loop body takes 1 step)
- 1 step for the return statement
Result in $k + 2$ steps for the non-recursive cost of each branch
The number of subtrees changes for each recursive call $k$ is not constant, so CANNOT do simple multiplication. Instead, write the steps into a tree
Adding up (separate num of $k$ and num of $+ 2$ )
- Sum of all subtrees ( $k$ ) is 9, one less the total number of elements (because each non-root item has exactly one parent, it is counted in exactly one subtree)
- Sum of all $+ 2$ s is the constant number of steps (2) times the number of recursive calls, which is equal tot he number of items (10). $2 \times 1 = 20$
- Total is $9 + 20 = 29$ steps

Generalize

For non-empty trees of any size. Let $n \in Z^{+}$ , assume the tree has the size $n$ , then there will be $n$ recursive calls been made
- The “constant time” part of the steps takes $2 n$ across all of the recursive calls
- The total number of steps taken by the for loop across al recursive calls is the sum of all the numbers of the children of each node, which is $n - 1$
**The total running time of $2 n + (n - 1) = 3 n - 1$ , which is $Θ (n)$ **

MEL.ZHU

Explorer

blogs

ENG

UofT Notes

ANT100

COG250

CSC111

MAT223

MGT100

PSY220

PSY230

PSY240

PSY260

PSY322

PSY424

STA130

CSC111: 3_Trees

Trees

Definition and Terminology

Tree implementation

Tree recursion

Ex. Tree size

Ex. `Tree.str`

Traversal orders

Mutating Trees (value-based deletion)

Running-Time Analysis for Tree Operations

Analyzing `Tree.len`

Analyzing the structure of recursive calls

Analyzing the non-recursive part of each call

Generalize

Graph View

Table of Contents

Backlinks

MEL.ZHU

Explorer

blogs

ENG

UofT Notes

ANT100

COG250

CSC111

MAT223

MGT100

PSY220

PSY230

PSY240

PSY260

PSY322

PSY424

STA130

CSC111: 3_Trees

Trees §

Definition and Terminology §

Tree implementation §

Tree recursion §

Ex. Tree size §

Ex. Tree.__str__ §

Traversal orders §

Mutating Trees (value-based deletion) §

Running-Time Analysis for Tree Operations §

Analyzing Tree.__len__ §

Analyzing the structure of recursive calls §

Analyzing the non-recursive part of each call §

Generalize §

Graph View

Table of Contents

Backlinks

Trees

Definition and Terminology

Tree implementation

Tree recursion

Ex. Tree size

Ex. `Tree.str`

Traversal orders

Mutating Trees (value-based deletion)

Running-Time Analysis for Tree Operations

Analyzing `Tree.len`

Analyzing the structure of recursive calls

Analyzing the non-recursive part of each call

Generalize